常用电工基础知识第三节第二课

三、典型的单相交流电路

1.纯电阻电路

负载是纯电阻的交流电路称为纯电阻电路，例如，负载为白炽灯、电热器等。

 1）电流与电压的关系

图2 -20为纯电阻电路的接线图和相量图。

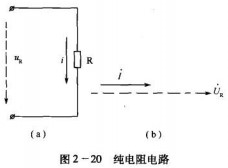
当电阻上流过电流i=Imsinωt时，电阻R的端电压为U=Imsinωt=Umsinωt

式中Um=ImR

等式两边同除√2，得U=IR

根据上述结论可知：

（1)电流与电压同相。

（2电流频率与电压频率相同。

（3电流与电压关系符合欧姆定律。

2）纯电阻电路的功率

在纯电阻电路中，电流、电压都是随时间变化的，由功率与电压、电流的关系可知，功率也是随时间变化的。瞬时功率等于电压瞬时值u与电流瞬时值i的乘积，即p =ui

根据公式，把同一瞬间的电压值与电流值逐点相乘，就可画出如图2-21所示的瞬时功率曲线。在前半周内，电压、电流均为正值，所以瞬时功率为正值;在后半周内，电压、电流均为负值，但相乘之后仍为正，所以瞬时功率为正值。由以上结论可知，不论电流方向如何，电阻总要消耗功率。

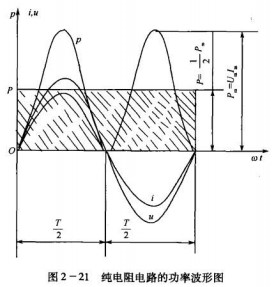
在瞬时功率曲线上一个周期内的平均值叫做平均功率。因为这个功率是电阻消耗掉的， 所以也叫有功功率，用P 表示，单位为瓦（W）。经数学推算可知，有功功率等于最大瞬时功率 的1/2,即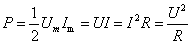

式中U—电阻上交流电压的有效值（V）

I——流过电阻的交流电流有效值(A)；

R——用电器的电阻(Ω)。

可见,此表达式与直流电路计算功率的公式形式一样.只不过电压、电流均为有效值。

2.纯电感电路

1)电压与电流的用位关系

由电阻近似为零的电感线圈组成的交流电路，可近试认为纯电感电路。

电感线圈的基本特点是：当通过电感线圈的电流发生变化时，在电感线圈中就要产生自感电动势，这个自感电动势的作用是阻碍电感线圈中电流的变化。其自感电动势与电流的变化率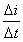成正比，即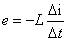

这里先说明一下，电流变化率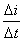。图2-22(b)为正弦电流波形的正半周，把时间轴以∆t等分，然后作垂直于时间轴的垂线与正弦电流波相交.从各交点作时间轴的平行线.即得到各段所对应的∆t;把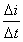称为电流的变化率。

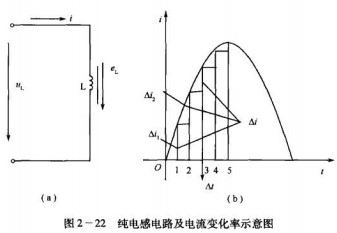
由图2 -22可见，在正弦电流波起始点，当时间变化第一个∆t时，电流变化了 ∆i₁,.其变化率为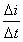；当时间变化第二个∆t.时电流变化了∆t₂.其变化率为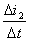。由于∆t相等.∆i₁>∆t₂, 所以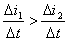在正弦电流波最大值时，∆t₅=0,即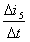变化率接近于零。下半周情况类似,只是电流变化率为负值。由上面的分析可知，正弦电流的波形从零开始上升.电流变化率最大.以后逐渐减 小,到正弦交流电出现最大值时，电流变化率为零。

假设电感线圈中通入正弦交流电流，其初相角为零，其电路图与波形图如图 2- 23所示。

把电流变化分为以下4个阶段：

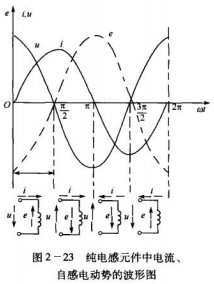(1)当ωt从0变化到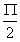时，电流为正，其数值不断增加，电流变率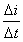为正，且不断变小，自感电动势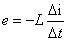为负，其绝对值逐渐减小，直到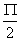处时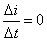，自感电动势e也为零。

(2)当ωt从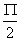变化到Π时，电流为正，其数值不断减小，电流变化率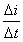为负，其绝对值逐渐增大，自感电动势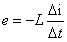为正值，不断增大，直到Π时为最大自感电动势也为最大。

(3)当ωt从Π变化到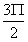时,电流从零变化到负的最大，电流变化率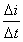为负，且从负的最大变化到零.自感电动势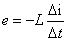从正值大变化到零，其方向与电流方向相反。

(4)当ωt从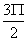变化到2Π时，电流从负最大变化到零，电流变化率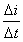为正，并且从零变化到最大值，自感电势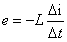从零变化到负最大,其方向与电流相同。在图2-23中，用虚线表示自感电动势的波形，可见自感电动势落后于电流90°。在纯电感电路中电阻为零,因此电源电压在任何一瞬间都与自感电动势大小相等、方向相反，所以u与e反相,U的波形

用实线表示(图2 -23)，显然电压超前电流90°，三者的相量关系如图2 -24所示。

2)电流和电压的关系

由于在电感线圈两端的电压相位不同于电流，所以不能用欧姆定律处理瞬时值的电压与 电流的关系。为了分析电感线圈中电压与电流的关系，我们做如下试验：

将一个电阻极小的电感线圈L与交流电源接通，改变交流电压数值，用电压表和电流表分别测量电感线圈两端的电压与电流，其测量数据见表2-2。

可以发现:电压有效值增大时,电流随着增加;电压有效值减小时，电流随着减小。

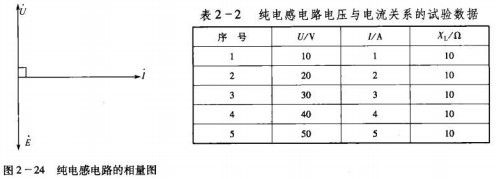
从表中数据可见:电感线圈中，电压有效值与电流有效值之比为一常数，用XL来表示这一 常数，即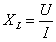

或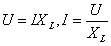

由此可见，此形式与欧姆定律一致。XL和电阻R相似，在纯电感电路中阻碍电流通过，把它叫做感抗,其单位也是欧姆(Ω)。

进一步的试验与数学推导证明，感抗和电感量与频率的乘积成正比，即

XL=ωL=2Πft

式中L—线圈的电感量(H);

F—电源电压的频率(Hz);

Ω—电源电压的角频率(rad/s)=2Πf

3)纯电感电路的功率

在纯电感电路中，电压瞬时值与电流瞬时值的乘积叫做瞬时功率，即Pₗ=uₗiₗ，如果把纯 电感电路中的电压值和电流值逐点相乘，就可画出如图2-25所示的瞬时功率波形。

由图可见，瞬时功率P以2倍的电源频率按正弦规律变化。从数学推导可知:瞬时功率的最大值为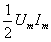，但在一周内的平均值为零，即纯电感电路中不消耗能量。用图2-25中瞬时功率波形从能量的角度来解释其含义。

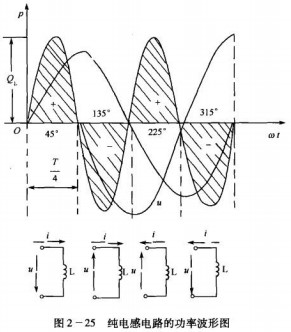
在电流的第一个1/4周期内，电流由零开始上升，此时在线圈周围逐渐建立起磁场。线圈 从电源中得到能量转化为磁场能量储存起来。在这段时间内电流与电压同方向，功率为正，表示线圈从电源吸取能量。

(2)在电流的第二个1/4周期内，电流由最大值逐渐下降到零，这时，原来储存在磁场中 的能量逐渐转化为电能而返还电源。这段时间内，电流与电压方向相反，功率为负，表示线圈向电源返还能量。

(3)在电流的第三个1/4周期与第一个1/4周期相似，虽然这时电流为负，但线圈中只要 有电流流过就会建立磁场，所以这段时间仍然是建立磁场储存能量过程,只是磁场方向相反. 由于电压与电流均为负.功率为正，说明线圈从电源吸收能量。

(4)在电流的第四个1/4周期与第二个1/4周期情况相似，也是线圈向电源送还能量。

上面的事实说明：在纯电感电路中，只有线圈与电源间的能量交换而没有能量的消耗。

通常用瞬时功率的最大值来说明能量转换的规模，并把它叫做无功功率，用QL来表示， 单位是乏(Var)。即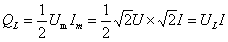

无功功率绝对不是无用的功率.它是具有电感的设备正常工作必不可少的条件。

无功功率在电力供电系统中有很重要的作用。电力供电系统中的许多电气设备(如变压 器、电动机等)都是具有电感性质的负载，它们要依靠磁场来传递能量，没有磁场它们就无法工作;要建立磁场，就必须从电源取得电能。因此,发电机必须向电感负载提供一定数量的无功功率。